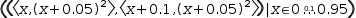7.6 Parametric sequences
Section §7.5 shows how parametric equations can be realized as Myron tuple generators. Given a sequence of points, the plotter draws line segments between them. When they are close together, a continuously connected sequence of points provides a visual approximation of a curve. This section shows how collection generators are used to provide sequences of points to the plotter.
The following interpretations are used.
- A point is determined by any composite value with 2 or 3 components. Complex numbers are naturally restricted to 2 components. Radial values are transformed to vectors as they are plotted.
- A tuple of points provides a sequence of points.
- A sequence that consists of exactly one point is drawn as a position vector. That is, a line is drawn from the origin to the point.
- A set does not define a sequence. Elements of a set or set generator, whether sequences or points, are treated as separate graphical elements.
To illustrate the effects, consider the difference between
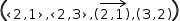
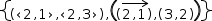
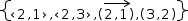
7.6.1 Simple Expression
The simple plot displayed for an expression like
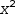
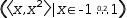

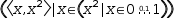
7.6.2 Segmented Circle
The parametric range control in Figure
7.11
draws part of a circle. A tuple of vectors generated over a range

A more elaborate example is given by a circle displayed as dashed lines. It can be plotted from
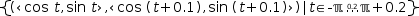
(1)
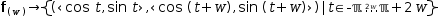
(2)
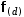
The dashed circle can also be displayed using nested generators, the inner for a dash and the outer for the sequence of dashes:
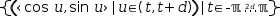
(3)
7.6.3 Quadrature Diagram
The standard diagram for quadrature shows same-width rectangles whose height is given by a function. The diagram is used to show how the area under a curve can be approximated numerically by adding the areas of the rectangles. The diagram is given in Figure 7.12.
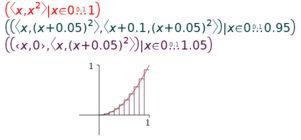
The plot in Figure
7.12
displays three separate expressions: two with disjoint line segments
and one with joined line segments. The latter is the easiest, being
given by
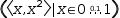
The horizontal lines are given by x-y pairs whose y value is the same:
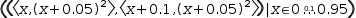
The vertical lines are given by x-y pairs whose x value is the same: